八皇后问题是一个以国际象棋为背景的问题:如何能够在8×8的国际象棋棋盘上放置八个皇后,使得任何一个皇后都无法直接吃掉其他的皇后?为了达到此目的,任两个皇后都不能处于同一条横行、纵行或斜线上。八皇后问题可以推广为更一般的n皇后摆放问题:这时棋盘的大小变为n×n,而皇后个数也变成n。当且仅当n = 1或n ≥ 4时问题有解。
关于这个问题更详细的描述可以参见维基百科1 ,使用Python的生成器(即含有yield语句的函数)来解这个问题就会变得很简单,15行以内python代码就可以解决这个问题,对于皇后的个数 n < 8 来说还是非常快的,只是当数量上升到很多的时候,这个解法就会非常的慢。不过这里仍然只讨论最简单的解法,后面会顺便提一下更高效的解法,比如16个皇后的情况在我的机器上只需要18秒。
下面是这个解法的完整的代码:
def conflict(state, nextX):
nextY = len(state)
for i in range(nextY):
if abs(state[i] - nextX) in (0, nextY - i):
return True
return False
def queens(num=8, state=()):
for pos in range(num):
if not conflict(state, pos):
if len(state) == num - 1 :
yield (pos,)
else:
for result in queens(num, state+(pos,)):
yield (pos,) + result上面这段代码关键点有3个,分别是冲突判断(即放置当前皇后位置的时候不能和已存在的皇后有冲突)、递归(遍历所有的情况要用到的方法)和yield表达式(保存遍历的结果的迭代器)。
冲突检测函数 conflict 的两个参数分别表示: 已存在的皇后的位置和将要放置的皇后的位置(即下一行中皇后的位置),冲突的条件就是,和已存在的皇后在同一垂直线上( state[i] - nextX == 0 )或者在对角线上( state[i] - nextX == nextY - i )。
递归函数是通过回溯法来求的每一种可能的情况,这个递归结束的条件是最后一个皇后能够无冲突的找到位置,然后从最后一个皇后的位置一次递归的向上层返回值,同时加上本层的皇后的位置,返回到最上层的时候即完成一次迭代( next() 函数调用一次),并且会记住当前的位置,下次继续迭代的时候会接着继续进行(这个其实是yield的特性)。
yield语句,在这里可以简单但当作储存返回值的一个元组或者列表来理解(实际上是一个迭代器,稍微有点复杂,后面会具体讲到),这里一次完整的递归(从 yield (pos, ) 这句返回到最上层调用)生成一种可能的情况(序列),也即迭代器的一项(对应于一种满足要求的所有皇后的摆法),在yield的使用迭代过程中,隐式或显式的调用一次next函数即执行一次完整的递归。;-)
yield 语句
yield的用法单独说一下是因为这个是理解上面的代码的关键,同时也是不好弄清楚的一个东西,这里 是一个关于yield的几行代码的使用例子。
从概念上说,yield是包含在Python的生成器里面的,相关的概念定义如下: > 生成器是一种用普通的函数语法定义的迭代器。 > > 任何包含yield语句的函数成为生成器2。
用下面这段常见的Python来辅助说明:
def fab(max):
a,b = 0,1
i = 0
while i < max:
yield a
a,b = b, a+b
i += 1
f = fab(5)
print f.next() # output: 0
print f.next() # output: 1
print f.next() # output: 1
print f.next() # output: 2
for i in fab(10):
print i, ',',
# output: 0 , 1 , 1 , 2 , 3 , 5 , 8 , 13 , 21 , 34 ,在上面的代码中,fab函数就是生成器,和普通的函数的区别在于:
- 不调用next方法,它不会自动执行;
- 每次调用next方法时只执行到yield语句处,然后挂起,等待下一次next的调用;
- 下一次调用next方法时,从yield的下一句开始执行,直到执行到yield语句,然后循环2-3的操作。
上面代码中的输出情况就表明了这样的过程,对于上面的 for 循环来说,for 循环里面的函数是隐式调用了所有的next方法,生成了一个列表(list),在for循环中的 fab(10) 是和 list(fab(10)) 等价的,可以用 print list(fab((10)) 看输出结果加以验证。
Debug 上面代码
如果觉得上面的代码很难理解,可以用单步执行的方式去跟踪和调试代码,同时使用 print 大法也是很有效果的。关于 step by step 的工具,可以使用 PyCharm 或者 Eclipse + Pydev 这两个IDE,或者也可以使用 pdb 这个工具,pdb和gdb的使用命令没有多大差别,所以如果是常用gdb来调代码的话,用pdb是毫无障碍的,当然,用这些工具的时候可以适时的配合几句 print 来会更好一些,上面三种,我个人还是推荐使用IDE(即PyCharm或者Pydev),因为有些功能还是那些面向指令集的调试器(比如pdb)没法比的.
通过单步跟踪之后,对yield的执行过程和上面的代码的递归调用栈应该就比较清楚了。
高效的八皇后问题解法
这段代码是用C语言写的,用了语言特性的位操作等,所以比python的快很多,对于小于等于16个皇后来说,这段C代码的实现比上面15行的Python代码实现快了好几个数据量级。
具体的代码请查看这里 : https://github.com/karottc/practice/blob/master/python/eight_empress.c .
这是在我的机器上的运行时间的截图:
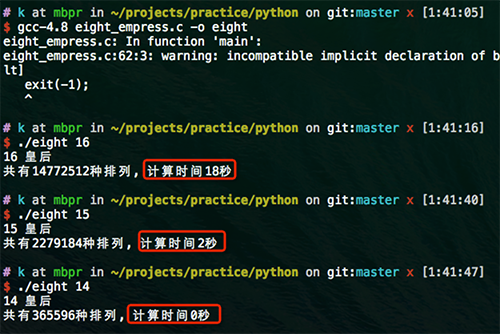
2014.07.10
Footnotes:
1 这个问题的两处描述分别是中文维基 和 英文维基, 推荐看英文的,因为英文的更详尽,中文相比英文版的维基百科的内容太少,对这个问题的描述一半都不到。
2 引用自《Python基础教程(第二版)》。